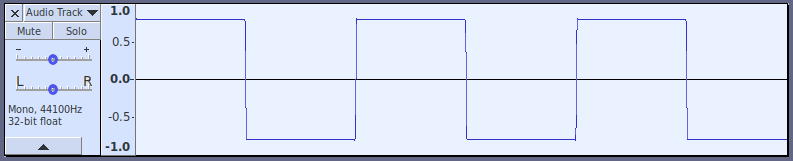
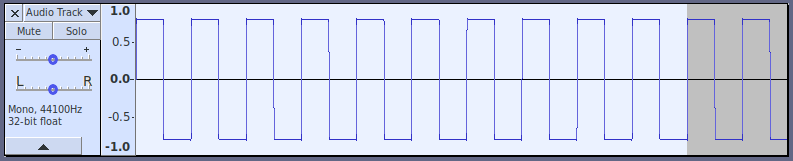
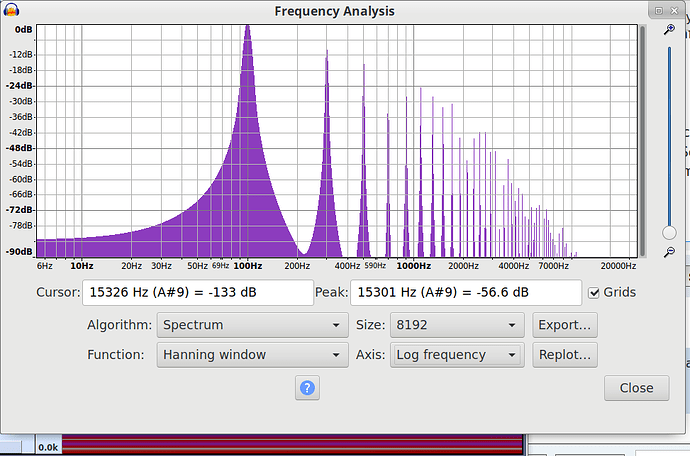
Audacity has a scripting language built in called “Nyquist”. It is very good for this sort of thing.
Here’s an example script that sums the first 8 harmonics of a “square” wave:
;version 4
(setf harmonics 8) ;number of harmonics
(setf hz 100) ;fundamental frequency
(setf wave (s-rest 1))
(setf amp 0.5)
(dotimes (hnum harmonics wave)
(setf f (* hz (+ 1 (* hnum 2))))
(setf amplitude (* amp (/ 1.0 (+ 1 (* hnum 2)))))
(setf wave (sum wave (mult (hzosc f) amplitude))))
You can run this in the Nyquist Prompt effect, by copying and pasting.
Some brief explanation:
A semicolon indicates the start of a comment. Comments are ignored by Nyquist.
The first line (;version 4) is a special comment that tells Audacity that we are using version 4 syntax. It is not strictly necessary in this case, but it’s good practice to include the syntax version number.
“Nyquist” is based on the LISP language. Functions are always written as:
(function-name arguments)
For example, where we would normally write:
2 + 3
In LISP / Nyquist, we write:
(+ 2 3)
“setf” is an assignment function. It sets the value of the first argument, to the value of the second argument.
Example:
(setf A 4) ;sets the value of 'A' to 4
(print A) ;prints 4
When a Nyquist script runs in Audacity, the final result is returned to Audacity. In this case, the returned value is a sound which I have called ‘wave’.
Here’s an overly commented version of the script:
;version 4
(setf harmonics 8) ;number of harmonics
(setf hz 100) ;fundamental frequency
;; Begin with "duration" of silence
(setf wave (s-rest 1))
;; and an initial amplitude of 0.5
(setf amp 0.5)
;; Add the sine tones
;; 'hnum' is the harmonic counter, and we increment it,
;; starting from zero, on each loop, up to the value of 'harmonics',
;; and return 'wave'.
(dotimes (hnum harmonics wave)
; Calculate required frequency:
(setf f (* hz (+ 1 (* hnum 2))))
(print f) ;prints the frequency to the debug output
; Calculate the required amplitude:
(setf amplitude (* amp (/ 1.0 (+ 1 (* hnum 2)))))
;; Generate the new sine wave and add it to 'wave'
(setf wave (sum wave (mult (hzosc f) amplitude))))