follow up How to generate arbitrary waveforms

DERF · December 14, 2017, 5:11pm

Hello. I have a question to ask.

(setf adsr (pwlv      0
                 0.05 1 
                 0.3  0.4 
                 0.5  0.4 
                 1    0))
(setq wiggle 0.3)
(setq wigglerate 3)
(setf envelope
  (sim (mult adsr (- 1 (* 2 wiggle)))
    (mult adsr wiggle  (sum 1 (hzosc wigglerate)))))
(mult envelope s)

The operator’ s manual say: "(sim [beh1 beh2 …]) Returns a sound which is the sum of the given behaviors…)
my question is the following one:in this code

 (sim (mult adsr (- 1 (* 2 wiggle)))
      (mult adsr wiggle  (sum 1 (hzosc wigglerate))))

_ the first behavior is:

 (mult adsr (- 1 (* 2 wiggle))

_ the second behavior is:

 (mult adsr wiggle  (sum 1 (hzosc wigglerate)))

Does it right?
Thank you.

steve · December 14, 2017, 5:40pm

Yes.

DERF · December 15, 2017, 5:02am

Thank you.
I would like to ask a second question.
She concerns the two behaviors exactly.
When we use without the function

(sim

the second behavior, we obtain the sound wave n°2. If we use 2 behaviors, we obtain the sound wave n° 1.
We observe a small difference.The intensity decreased, and the wave is not altered in the same way all the time (the drawing of the wave is different) in the wave n° 2.The shape is more regular.
My question is the following one: is there an article which explains how the 1ier behavior acts on the second, and finally, which is the interest to combine behaviors, as in this precise example.

Thank you for your help
BEHAVIORS .jpg

steve · December 15, 2017, 11:25am

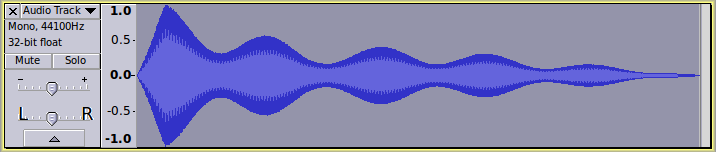
I’ll split up your code into sections, and demonstrate what each bit does:

(setf adsr (pwlv 0 0.05 1 0.3  0.4 0.5  0.4 1 0))

This creates an “envelope”, which is a low sample rate control signal.
A “control signal” is just a “sound”, but at a low sample rate, and changing much more slowly that a normal audio waveform.

By default, “PWLV” creates control signals (“sounds”) that have a sample rate 1/20th of the track sample rate.
If you return this kind of “sound”, on it’s own, back to the Audacity track, the length of the sound will be 1/20th of the length that you generated.
The sound returned by PWLV is assigned as the value of “adsr”.

Example,

(pwlv 0 0.05 1 0.3 0.4 0.5 0.4 1 0) creates a signal that has length “1”.
If this is in a “generate” type effect (in the Generate menu), then that is “1 second”.
If this is in a “process” type effect (in the "Effect menu), then “1 unit” of time gets stretch to equal the length of the selection.

The “Nyquist Prompt” is, by default, a “process” type effect, so running this command in the Nyquist Prompt will return as sound that is 1/20th of the length of the selection:

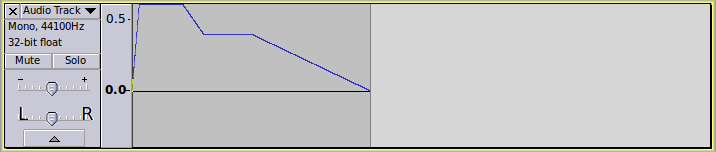
(setq wigglerate 3)
(hzosc wigglerate)

HZOSC generates a sine wave at the specified frequency, which in this case is 3Hz. The sample rate of the Audacity track is used.
The default duration is 1 second, which when run in a process type effect is mapped to the length of the selection:

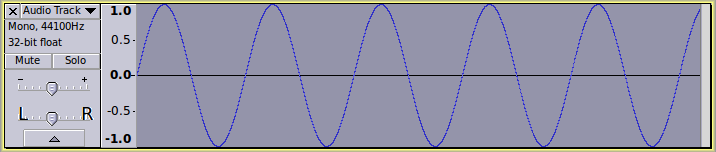
(setq wigglerate 3)
(sum 1 (hzosc wigglerate))

Adding “1” to the sine wave, offsets it vertically, so that it has a range of 0 to 2.
I have zoomed out vertically so that you can see the top part of the waveform:

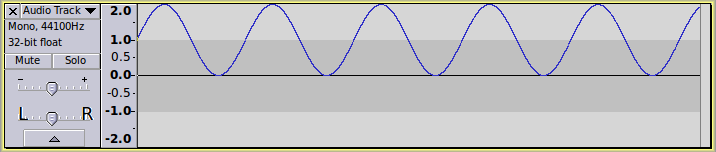
(setq wiggle 0.3)
(setq wigglerate 3)
(setf adsr (pwlv 0 0.05 1 0.3  0.4 0.5  0.4 1 0))
(mult adsr wiggle  (sum 1 (hzosc wigglerate)))

Here we have generated a low frequency control signal “adsr”, and a 3Hz sine wave which is offset vertically, and then we are combining them by multiplication.

Nyquist is clever here, because although the sample rate of adsr does not match the sample rate of the sine wave, Nyquist can handle that and uses the length in seconds, which in both cases is “1”. However, if we are running this in the Nyquist Prompt, 1 second is mapped to the length of the selection.

Each sample in the sine wave is scaled (multiplied) by the value of adsr at the corresponding time.

Note that we are multiplying three things:

the control signal “adsr”,
a constant value “wiggle”, which is = 0.3
the sine wave (hzosc wigglerate)

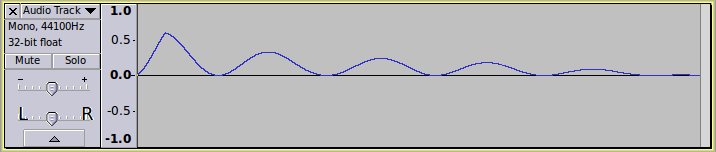
(- 1 (* 2 wiggle))

This part is a bit of a distraction. “wiggle” is just the value 0.3, so the above expression simply evaluates to:
1 - (2 * 0.3)
= 0.4

so this:

(mult adsr (- 1 (* 2 wiggle)))

could be written more simply as:

(mult adsr 0.4)

which gives us:

SIM is the same as SUM, and is simply a function for adding signals or numbers.

(setf adsr (pwlv 0 0.05 1 0.3  0.4 0.5  0.4 1 0))
(setq wiggle 0.3)
(setq wigglerate 3)

(setf envelope
  (sim 
    (mult adsr (- 1 (* 2 wiggle)))
    (mult adsr wiggle  (sum 1 (hzosc wigglerate)))))

So here we are adding the envelope (mult adsr 0.4), with the wiggly line created in the final line, and assigning the result as the value if ENVELOPE:

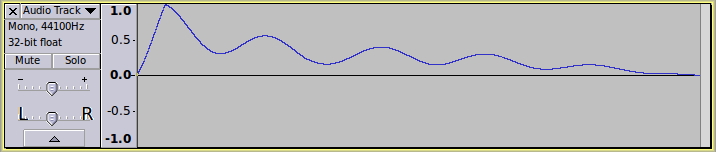
We can now multiply this envelope with any sound that we like. In the initial code, it multiplies the envelope by the sound from the Audacity track “S”. Alternatively you could generate a sound, and multiply (scale) it with the envelope, for example, here I generate a 440 Hz sawtooth waveform, and multiply it by the envelope:

(setf adsr (pwlv 0 0.05 1 0.3  0.4 0.5  0.4 1 0))
(setq wiggle 0.3)
(setq wigglerate 3)

(setf envelope
  (sim 
    (mult adsr (- 1 (* 2 wiggle)))
    (mult adsr wiggle  (sum 1 (hzosc wigglerate)))))

(setf my-saw-waveform (osc (hz-to-step 440) 1 *saw-table*))
(mult envelope my-saw-waveform)

DERF · December 16, 2017, 8:16am

Thank you very much.
It is very interesting.

DERF · December 17, 2017, 10:54am

Hello.
It is necessary to begin with this code:

(push (/ (+ 1.0 count) num) point-list )

My question is the following one: Is the following code identical to the first one?

(setf point-list (cons (/ (+ 1.0 count) num) point-list))

It is right?
Thank you.

steve · December 17, 2017, 11:28am

(setf a '(1)) ; A list containing the number 1
(setf b (push 2 a))
(setf c (cons 3 a))
(print a) (print b) (print c)

(setf a (cons 4 a))
(print a)

prints to the debug window:

(2 1)
(2 1)
(3 2 1)
(4 2 1)

PUSH added “2” to the list A, modifying A, so A = (2, 1)
B = A, so B also = (2, 1)

CONS adds “3” to the list and returns the extended list, but does not modify the list,
C = (3, 2, 1), but A is still = (2, 1)

(setf a (cons 4 a)) adds “4” to the list, and sets A to the returned value of CONS, so A now = (4, 2, 1)

More about CONS: http://www.audacity-forum.de/download/edgar/nyquist/nyquist-doc/xlisp/xlisp-ref/xlisp-ref-080.htm
More about PUSH: http://www.audacity-forum.de/download/edgar/nyquist/nyquist-doc/manual/part11.html#index791

DERF · December 18, 2017, 6:00pm

Thank you.
It is necessary to leave the following code:

(setf point-list  '(list 0.1 0.5  1 0))
(setf amp-list (list 0.1  0.8  0.2  0.8   0.1  1 0))
(setf num (1- (length amp-list)))

(dotimes (count   num)
(setf a  (push (nth (1+ count) amp-list) point-list)))

(print a)
return : (0  1  0.1  0.8  0.2  0.8 LIST 0.1 0.5 1 0)

I tried to explain.
It seems to me that:
_ “num” take this “value”: 6
_ “count” takes successively the “value” (0 - 1- 2- 3 - 4 - 5 )

My question is the following one:
Why does the evaluation proceed upside down?
[nth] takes successively the values 5 4 3 2 1 0.

(push (nth (1+ 5) amp-list) point-list))

If you write this code

(setf a (nth 6 '( 0.1  0.8  0.2  0.8   0.1  1 0    )))

(print a)

LISP return “0”
Then:

(push (nth (1+ 4) amp-list) point-list))

return the value “1”
and so on.
Thank you for your reply.

steve · December 19, 2017, 1:04am

It doesn’t.

Let me give an example:

(setf a-list (list "A" "B" "C" "D"))  ; a list containing letters
(setf num (length a-list))  ; set NUM to the length of the list
(print num)         ; prints 4 to debug window
(terpri)            ; new line
(setf new-list ())  ; an empty list

(dotimes (count num)    ; loop where "count" takes values 0 to 4
  (setf val (nth count a-list))   ; set VAL to the nth item in A-LIST
  (format t "Item ~a in a-list = ~a~%" count val) ; prints the value of the nth term in A-List
  (push val new-list)   ; push the value to the begining of NEW-LIST
  (format t "NEW-LISt = ~a~%" new-list) ; print NEW-LIST
  (terpri))             ; new line

The debug window shows:

4

Item 0 in a-list = A
NEW-LISt = (A)

Item 1 in a-list = B
NEW-LISt = (B A)

Item 2 in a-list = C
NEW-LISt = (C B A)

Item 3 in a-list = D
NEW-LISt = (D C B A)

Note that PUSH adds the value to the start of the new list, so the new list is the reverse of the original list.

DERF · January 1, 2018, 5:28pm

Thank you.
It concerns the function [(format].
We can write:

(format nil "~s ho ho" "o&&")

But, we can also write:

(format t "~s ho ho" "o&&")

The answer of the nyquist prompt is identical.
My question is this: Is there a difference nevertheless?
Thank you for your response.

steve · January 1, 2018, 6:15pm

The “format” function prints an expression to the specified ‘destination’ (http://www.audacity-forum.de/download/edgar/nyquist/nyquist-doc/xlisp/xlisp-ref/xlisp-ref-121.htm)
If the ‘destination’ is NIL , a string is created and returned with the contents of the ‘format’.

If a Nyquist script returns a string, then Audacity displays the string in a pop-up message window.

In LISP / Nyquist, the tilde “~” character in a string has a special meaning. In conjunction with the next character, it acts as a “format specifier”.
Some common format directives are:
~A - Prints the expression as ASCII text. Strings are printed without quotes.
~S - Prints the expression as an s-expr. Strings are printed with quotes.
~% - prints a ‘newline’ control character.

(format nil "~s ho ho" "o&&")

This will replace ~s with “o&&”, forming a string:
“o&&” ho ho

If the ~A specifier is used,

(format nil "~a ho ho" "o&&")

then the created string will be:
o&& ho ho

The returned string may be bound to a variable like this:

(setf my-string (format nil "~a ho ho" "o&&"))

Because the destination is NIL, the format function doesn’t print the string anywhere, but if the string is the final expression in a script, then the string will be the value that is returned by the script (the “return value”) and Audacity will display it in a pop-up message.

(setf my-string (format nil "~a ho ho" "o&&"))
(hzosc 440)

This code creates a string “o&& ho ho” and binds the value to the variable “my-string”. The string is not printed because the destination is NIL.
The return value of the script is a 440 Hz sine wave.

(setf my-string (format nil "~a ho ho" "o&&"))
(hzosc 440)
my-string

In this case, “my-string” is the final expression of the script, so it is returned to Audacity. The value of “my-string” is “o&& ho ho”, so Audacity creates a message window and displays the text “o&& ho ho” in it.

If the ‘destination’ is T , the printing occurs to standard-output. For Nyquist plug-ins, the standard-output is the debug window.

(setf my-string (format t "~a ho ho" "o&&"))
(hzosc 440)

This code creates a string “o&& ho ho” and binds the value to the variable “my-string”. The string is printed to the debug output.
The return value of the script is a 440 Hz sine wave.

(setf my-string (format t "~a ho ho" "o&&"))
(hzosc 440)
my-string

In this case, “my-string” is printed to the debug window.
“my-string” contains the string “o&& ho ho”, but it also carries the “destination” as the debug output, so it is not returned to Audacity so there is no message box.

If we want the last example to return “my-string” to Audacity as well as printing to the debug window, we could write:

(setf my-string (format nil "~a ho ho" "o&&"))
(format t "~a" my-string) ;print to debug
(hzosc 440)
my-string ;return value

DERF · January 3, 2018, 2:22pm

Thank you.
My question concerns ask functions (dotimes and format).
(dotimes (sym expr [rexpr]) expr…)
symbol = a symbol
end-expr = an integer

(format stream fmt arg…)
fmt = a string of custody

Now, it is necessary to observe this code:

(format t "Item ~a in a-list = ~a~%" count val)

In this case, we observe that the arguments are:“count” and “val”
But, “count” is a symbol.
My question is the following one: Can we use symbols as arguments of the function “format”?
Thank you for your answer.

steve · January 3, 2018, 3:00pm

If the symbol “count” has a value (if it is “bound”), and if that value can be represented as a string (most values can), then yes you can use it like that and the value bound to “count” will replace the associated “~a” in the string.

Example:

(dotimes (count 4)
  (format t "Counter is ~a~%" count))

Debug output:

Counter is 0
Counter is 1
Counter is 2
Counter is 3

DERF · January 6, 2018, 4:51pm

Thank you.
I have a question. it concerns the following function: terpri.
Into the code

(setf a-list (list "A" "B" "C" "D"))
 (setf num (length a-list))
(print num) 
 (terpri)

the print function prints correctly the value 4.
It seems to me that the function terpri prints objects awaiting impression.
But, in this example, the value 4 is already printed.
Thus, my question is the following one: what is the utility to use here the function terpri?
Beforehand thank you for your answer.

steve · January 6, 2018, 5:26pm

http://www.audacity-forum.de/download/edgar/nyquist/nyquist-doc/xlisp/xlisp-ref/xlisp-ref-279.htm
In short, TERPRI prints an EOL character.
(the name “terpri” comes from “terminate print”)

DERF · January 12, 2018, 5:46pm

Thank you.
I tried to use prin1 here

(setq data1 (list 0 0 1 1 0 1 1 0 0 1 1 0 0 0 1 0 1 0 0 0))
    (setq intvl 5)
    (setq root 60)

    (abs-env
     (simrep (i 4)
      (let*
       ((vol (* 8 (nth (+ 1 (* i 5)) data1)))) 
(prin1  (* i 5))
(prin1 (+ 1 (* i 5)))  )))

But, there is a problem. LISP return 015610111516
To use terpri

 (prin1  (* i 5)) (terpri)
(prin1 (+ 1 (* i 5)))    )))

does not solve the problem.

My question is this:
Why is the first evaluation 051015 mixed with second 161116?

steve · January 12, 2018, 7:23pm

(prin1  (* i 5)) (terpri)

That will print the result of (*i 5) and then print a new line.

(prin1 (+ 1 (* i 5)))    )))

That will print the result of (+ 1 (* i 5)) and returns the result. There is no new line.

so when i = 0, the loop will print:

0
1

when i = 1, the values 5 (new line) and 6 are printed directly after the “1” giving:

0
15
6

then when i = 2, the values 10 (new line) and 11, giving:

and so on.

If you use “print” instead of “prin1”:

(setq data1 (list 0 0 1 1 0 1 1 0 0 1 1 0 0 0 1 0 1 0 0 0))
(setq intvl 5)
(setq root 60)

(abs-env
  (simrep (i 4)
    (let ((vol (* 8 (nth (+ 1 (* i 5)) data1))))
      (print  (* i 5))
      (print (+ 1 (* i 5))))))

you will get:

DERF · January 13, 2018, 12:53pm

Thank you.
I tried to explain.
It is strange that LISP estimates first:
(0 X 5) - (1 + 0 X 5)
then (1 X 5) - (1 + (1 X 5) …
But not:
(0 X 5) - (1 X 5) - (2 X 5) - 3 X 5)
then (1 + 0 X 5) - (1 + (1 X 5) and so on
It is strange because the code is first:
(print (* i 5) then (print (+ 1 (* i 5))
It was my badly explained question.
So, my question is:
Can we write a code the evaluation of which gives:
051015
161116

Beforehand, thank you for your answer.

steve · January 13, 2018, 1:29pm

I don’t know what you are trying to achieve (you’ve not said).

If you want to produce two lists, one containing the numbers 0 5 10 15 and the other containing the numbers 1 6 11 16, then this will do it:

(let ((list-a ())
      (list-b()))
  (dotimes (i 4)
    (push  (* i 5) list-a)
    (push (+ 1 (* i 5)) list-b))
  (print (reverse list-a))
  (print (reverse list-b)))

DERF · January 17, 2018, 3:47pm

Hello.
Thank you for your post.
My problem concern let and let*.
Please read this code.

(setq a 'top) 
(defun dummy-function () a) 
 (let ((a 'inside)
       (b a))            
  (format nil "~S ~S ~S" a b (dummy-function)))

This code return “INSIDE TOP TOP”
I don’t understand this evaluation.
The first character S is linked to a. But, in the code, there are three “a”
a = top / a = inside / b = a (or a = b)

Apparently, it would seem that the function let creates an evaluation in parallel bindings.
I found some informations on the let function in COMMON LISP, but I realized that this language is very different from the LISP.

My question is the following one: Is there an article which explains that is an evaluation in parallel, or sequential.
Thank you for your help.