Any way to extract hidden audio from a file?

[steve]

I have been investigating those weird subliminal channels on youtube for a while (by following their interactions in comments, connections with businesses, etc) and have managed to get quite a lot of information.
However, I have hit a snag. I need to remove hidden text from one of these files, but I have no idea how to do it.
I really want to see what is in these so I can finally prove that the authors are fraudulent.

A lot of commonly seen “Silent Subliminals” use either “amplitude modulation” (“AM”) or (much less commonly) “frequency modulation” (“FM”) to encode the “message” in a very high frequency range (often around 16 - 17000 Hz). Although people that have excellent hearing may hear the encoded sound as a high pitched whistle, most people, and particularly adults, will not hear the sound at all because it is so high pitched.

The well known (amongst silent subliminal enthusiasts) “Lowerey” method (patented by O.M. Lowerey) uses amplitude modulation, which is akin to how AM radio works, except that the carrier frequency is a high frequency audio signal (typically around 16- 17 kHz) rather than radio frequency. Despite claims to the contrary, Lowerey O.M. Lowerey’s work was not in the slightest bit “scientific” as it completely lacked any testable hypothesis concerning a mechanism that would allow a person to “subconsciously hear” sounds above their hearing range, let alone how they could subconsciously decode an amplitude modulated signal. Nevertheless, it is still possible to detect and decode audio frequency AM encoded messages, if we know what to look for and have the technology (such as “Audacity”) to decode it.

The way to create audio frequency AM modulation is described in this post: Silent Subliminals [solved?]
Basically, there are two steps:

1. Filter the “message” audio so that it has a frequency range that is no more than the range between “half the sample rate” and the carrier frequency.
   Example, if the track sample rate is 44100 Hz, then half the sample rate (also known as the “Nyquist Frequency”) is 22050 Hz. If the carrier wave has a frequency of 17000 Hz (17 kHz), then the range between the carrier frequency and the Nyquist frequency is:
   22050 - 17000 = 5050
   So the “message” audio must be filtered to remove frequencies above 5050 Hz.
2. Modulate (multiply) the filtered message by a sine wave at the carrier frequency.
   This does the actual “modulation”.
3. An optional third step is to filter out the carrier frequency and / or frequencies below the carrier frequency.
   The modulated signal is essentially symmetrical around the carrier frequency, so by removing the lower half (which is much easier to hear because it is not such high frequencies) the modulated signal can be made less audible.

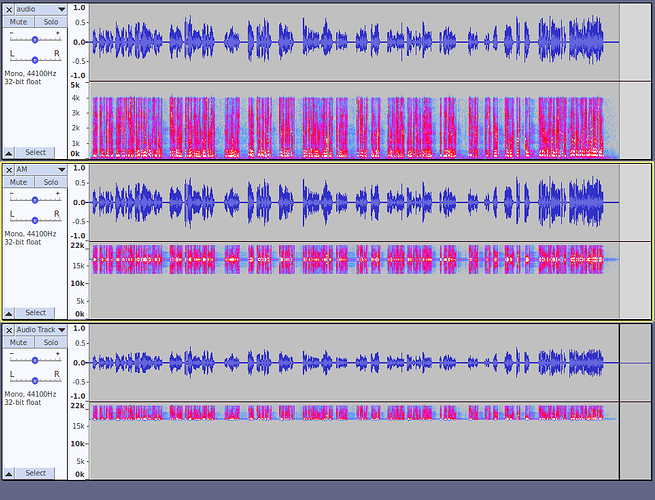
The three tracks shown below illustrate what each step looks like as both waveforms and spectrograms (frequency plots).

1. The top track shows a voice recording that has been filtered with a very steep filter at 4000 Hz.
2. The middle track shows the audio after it has been modulated by a 17000 Hz carrier. Note that the lower half below 17000 Hz is a mirror reflection of the half above 17000 Hz.
3. The third track is after the track has been filtered again to remove the carrier and all lower frequencies.

If an audio file contains an AM encoded message, you will see a high frequency waveform within the spectrogram that looks similar to either the second of third tracks above.

Once detected, it can be decoded back to the original audio by “de-modulation”. For AM, this is quite easy (with the appropriate tools, such as Audacity) and is similar to encoding. There are again 2 steps:

1. Multiply the AM signal by the carrier frequency.
   This will create two new waveforms with frequencies in the ranges as shown below. The lower range is the actual audio, and the upper range is a kind of reflection.
2. Filter out the reflection with a very steep low-pass filter.

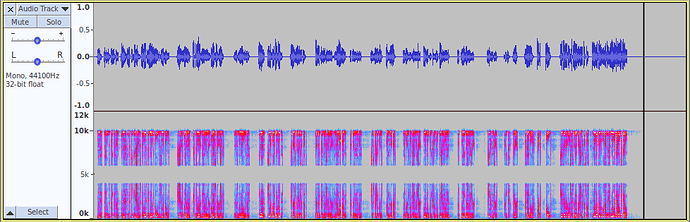
This final image shows the AM signal from the first test after it has been demodulated (but not filtered).
Notice there are two frequency bands: 0 to 4000 Hz (the same range as the original audio), and around 6000 to 10000 Hz (the “reflection”).

If the final low-pass filter is not applied, the result will still be audible, but it will sound a bit weird because of the reflection.

so…
the steps to determine if there is a “message”, encoded according to O.M. Lowerey’s patented method, and to hear what the “message” is:

1. Look for an AM signal.
2. Guess as closely as possible what the carrier frequency is (usually above 15000 Hz and below 18000 Hz)
3. Multiply the track by the carrier frequency (see below)
4. Optional, filter out the “reflection”

To “multiply” the waveform by a sine wave of a specific frequency, use the Nyquist Prompt effect, and enter code similar to this:

(mult *track* (hzosc 17000))

Change the number “17000” if necessary to match the carrier frequency that you determined from the waveform.


I hope that you find the above interesting and useful, but so as not to mislead you or others, I feel that I should include a disclaimer:

Disclaimer:
While I find the mechanics of audio frequency AM modulation / demodulation interesting, I find the idea that people can somehow “magically” capture sounds that are beyond their hearing range and subconsciously apply the necessary demodulation techniques (as described above) to decode the message, to be rather far fetched. Although in more recent times, hypotheses have been proposed to explain how it could occur, verifiable experimental evidence to support these new hypotheses is lacking. (I’m also being very loose with the term “hypotheses”, as in a scientific context a hypothesis is based on empirical evidence rather than being devised to explain a belief.)