Aliasing

[briandc]

Hi everyone,
I was wondering if Audacity can help detect (and remove) any possible aliasing. If not, what would be a good way to know if the digital audio I am producing has any aliasing in it (apart from what can obviously be heard)?

Thanks!

brian

[steve]

@briandc

what would be a good way to know if the digital audio I am producing has any aliasing in it

That depends on how you are producing the digital audio. If you are “recording” the audio directly into Audacity, then so long as your sound card is not creating aliasing distortion (if you’re using a reasonable sound card then it won’t), there will be no aliasing distortion. If you are digitally generating the audio. then there could be aliasing distortion, in which case you would need to compare the spectrum of the generated audio with the expected spectrum.

We can probably be more specific if you give more details.

[briandc]

@steve

That depends on how you are producing the digital audio. If you are “recording” the audio directly into Audacity, then so long as your sound card is not creating aliasing distortion (if you’re using a reasonable sound card then it won’t), there will be no aliasing distortion. If you are digitally generating the audio. then there could be aliasing distortion, in which case you would need to compare the spectrum of the generated audio with the expected spectrum.

We can probably be more specific if you give more details.

Sure; I’m doing digitally-generated audio. As I see you use Debian, an example of what I’m exploring is amSynth (I’m sure it’s available in your repos there too). Some of the presets definitely produce some aliasing, and I’m just trying to figure out where it comes from (oscillators, etc) and how to attenuate it (EQ, filters, other audio processing available in Audacity).


brian

[steve]

When generating audio you need to avoid aliasing rather than trying to fix it.

Aliasing distortion occurs when attempting to represent frequencies that are higher than the Nyquist frequency (half the sample rate). For example if you generate a 10 second “Chirp” from 400 Hz to 1000 Hz with “Waveform” set to “Square”, then when you listen to it you will hear a swooshing sound in the background. That swooshing is the aliasing distortion. Try as hard as you can and I doubt that you can get rid of it.

Now try the same again but with “Waveform” set to “Square, no alias”. Now you hear the sweeping tone but without the swooshing.

One way to minimize the amount of aliasing when generating sounds is to generate at a very high sample rate. This avoids most of the aliasing because the high sample rate means there is a high Nyquist frequency (half the sample rate) so most of the generated frequencies can be represented correctly. Try generating the first type of Chirp (“Square” waveform) but set the sample rate to 192000 first. Notice how the swooshing has almost completely disappeared. After generating, you can safely convert the sample rate back down to 44100 Hz - the resampler has anti-aliasing filters built in so reducing the sample rate in Audacity will not create aliasing (assuming that Audacity is set to use the default best quality resampling).

[briandc]

Hi Steve,
thanks for the info. Yes, I do processing at 48000 rather than 44100 in order to try to “keep the bar higher”. I don’t think my soundcard will accept 192000 though. That might be a good route to try, although some people say that it takes up too much CPU or other resources (I don’t know if that’s accurate though).

I understand that it’s better/more desirable to try to avoid aliasing rather than trying to eliminate it. Amsynth doesn’t have an anti-aliasing option, so I try to control the signal just by listening to the high-end notes for distorted signal, and then attenuating the filter depth and the filter key follow; or just by avoiding going too far in the high-end range.

But now I have a doubt: does Audacity record the audio signal before it reaches the soundcard, or after? My thinking until how has always been that the soundcard serves only for creating the final digital-to-analog signal for output.


brian

[steve]

Note that I described two ways to avoid aliasing.

“Oversampling” (using a much higher sample rate and then converting back down to a ‘normal’ sample rate) is one way. This works because the very high sample rate is able to handle much higher frequencies so no aliasing there, then downsampling (using anti-aliasing filters) removes the excessively high frequencies before converting. This approach is the only option if you can’t limit the frequency range before converting from analog to digital.

The other approach is to limit the frequency bandwidth of the generated signal. That’s how the chirp using “Square, no alias” manages to avoid aliasing. The frequency range of the sound being generated is limited to less than half the sample rate.

From this Wikipedia article: Aliasing - Wikipedia
This image helps to explain how aliasing occurs:

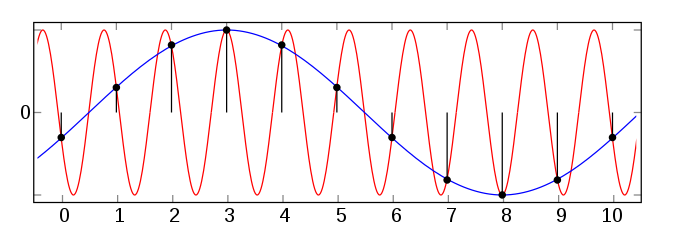
We can see that the above set of sample points can fit with two different sine waves. However, the red wave has a frequency that is higher than half the sample rate. The Nyquist Shannon theorem tells us that for any “band limited” signal, there is and can be only one (analog) signal that fits the dots. If we fed the red analog waveform directly into an A/D converter (analog to digital) and the sample rate on the digital side was as shown, then on playback (converting from digital to analog) we would hear the blue waveform. To prevent that from occurring, both A/D and D/A converters limit the bandwidth on the analog side to less than half the sample rate on the digital side. Thus, in all cases, there is only ever one possible waveform that will fit the sample values.

Here’s an experiment that shows what “bad things” can happen when synthesizing in the digital domain:

1. Set the Project Rate (bottom left corner of the Audacity window) to 88200.
2. Generate 4 tracks with sine waves at the following frequencies: 2000, 3000, 20000, 30000 (in this track order)
3. Combine the first two tracks (2000 and 3000) into one stereo track (Splitting and Joining Stereo Tracks - Audacity Manual)
4. Combine the second two tracks into a stereo track.
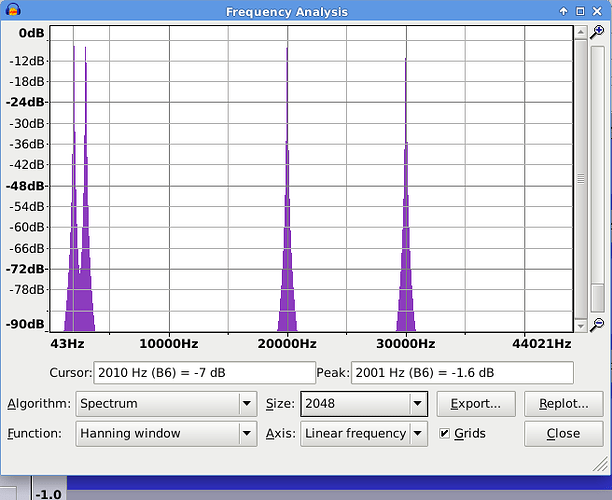
5. Select all and look at the spectrum:
   
   
   
   As expected, we have peaks at 2000, 3000, 20000 and 30000.

What happens if we modulate the left channel with the right channel? Amplitude modulation is equivalent to multiplication, and multiplying two sine tones will give us two new tones, one that is at the difference and the other at the sum of the two original frequencies. Thus what we would expect in the first track is:
2000 + 3000 = 5000 Hz
3000 - 2000 = 1000 Hz

and for the second track:
20000 + 30000 = 50000 Hz
30000 - 20000 = 10000 Hz

Let’s try doing this. Audacity does not have a built-in AM modulation effect, but it has a built-in scripting language called “Nyquist” which allows us to do almost anything (Missing features - Audacity Support).

6. Select both tracks, then using the “Nyquist Prompt” effect (Nyquist Prompt - Audacity Manual), apply this code:

(mult  (aref *track* 0) (aref *track* 1))

I’m assuming that you are using an up to date version of Audacity and that the “Use legacy (version 3) syntax” option is NOT selected.

The selected tracks are passed in turn to the Nyquist program and the code is applied.
In this code, track is the audio data from the selected track (tracks are processed one at a time).
(AREF TRACK 0) gives the left channel and (AREF TRACK 1) gives the right channel.
MULT is the command to multiply.
The result is passed back from Nyquist to Audacity and returned to the track. Because we are returning just one sound to a stereo track, Audacity copies the returned audio into both tracks.

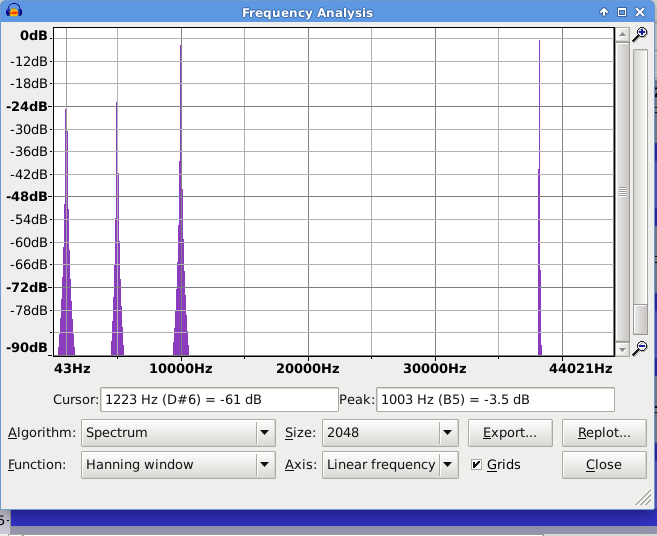
7. Look at the result in Plot Spectrum:
   
   
   
   As expected we have peaks at 1000 Hz and 5000 Hz, but in the second track we have peaks at 10000 Hz and 40000 Hz.
   The thing that went wrong (40k instead of 50k) is that our track sample rate is ‘only’ 88200 Hz, which means that the maximum possible frequency that can be represented is 44100 Hz, but we have calculated sample values that “should” have a frequency of 50000 Hz. As shown previously, this new data is ambiguous; not only would 50000 Hz fit the generated sample values, but so will 40000 Hz. 50000 Hz is not allowed, so we get a peak at 40000 Hz instead, and that is aliasing distortion.
   
   
   Moving on to the relevance of this to your question:

If you use a digital synthesizer that creates aliasing distortion in this way, then that is a fault / limitation of the synthesizer and there is nothing that you can do about it.

What the synthesizer code should do to ‘avoid’ this problem, is to use a sufficiently high sample rate internally (oversampling). It is not uncommon for high quality digital synths to oversample x8, that is, at 8 time the sample rate of the track, so for a 44100 Hz track, the synth could be working internally with sample rates as high as 352800 Hz.

I don’t know if amsynth uses oversampling. As it is intended for real-time use, it may not, in which case you can expect aliasing when generating high notes, but not a problem with bass notes.

@briandc

does Audacity record the audio signal before it reaches the soundcard, or after?

Audacity can do either. it depends on how your audio system is set up.

If you are using ALSA as the host and “pulse” as the input / output device, then the audio is routed through PulseAudio at whatever sample rate PulseAudio is using (usually 44100 or 48000 Hz).

If you are using ALSA as the host and one of the “hw” options as input/output, then they connect directly to the sound card via ALSA and the sample rate will be whatever your sound card chooses.

If you are using Jack Audio System as the host, then you can choose whether to connect to physical inputs / outputs or directly to the in/out ports of any application that exposes jack ports (any audio software that supports Jack). The sample rate will be whatever sample rate Jack is running at, which must be a rate that is supported by your hardware.