What are your thoughts about how to do that?
My thoughts about how to do that are to define a tone of 4000 Hz, create a new gain list for this frequncy, define a seperate function of shuffling for that. Create a tone-silence pair for this tones. Merge new list and new tones to the previous one in the function let. At the end merge the pair of tone-silence pair of the tones of 1000 Hz and shuffled list of amplitudes of the tones at 1000 Hz with the tone-silence pair of the tones of 4000 Hz and shuffled list of amplitudes of the tones at 4000 Hz.
How about something like this (in pseudo code):
DO [from pitch-type = 0 to pitch-type = 1]
{
IF [pitch-type == 0]
pitch = 1000
ELSE
pitch = 4000
DO [from gain = 0 to gain = -45 | gain = gain -5]
{
DO [10 times]
{
PUT (pitch, gain) INTO parameter-list
}
}
}
RETURN parameter-list
So what we end up with is a list of (pitch / gain) pairs, containing 10 of each gain level for each pitch (200 pairs in total).
and then shuffle that list.
We would then need to make a sequence of tones, drawing the gain and pitch from successive (pitch / gain) pairs.
Actually, this solution seems much more reasonable than my solution but it is hard for me to realise that in Nyquist. Could you give me some tips ?
Not guaranteed to be correct - this is off the cuff, so do check it:
;version 4
;type generate
;; Global variables. These could be set by user controls.
(setf minrest 1.8)
(setf maxrest 2.8)
(setf lohz 1000)
(setf hihz 4000)
(defun tone (pitch)
(mult (osc pitch 0.25)
(pwlv 0 0.02 1 0.23 1 0.25 0)))
(defun paramlist (&aux params)
"Return a list of (pitch gain) pairs"
(dotimes (noteid 2 params)
(setf pitch (if (= noteid 0)
(hz-to-step lohz)
(hz-to-step hihz)))
(do ((gain 0 (- gain 5)))
((= gain -50))
(dotimes (i 10)
(push (list pitch (db-to-linear gain))
params)))))
(defun shuffle (data)
"Shuffle a list"
(let ((n (length data)))
(do* ((i (1- n) (1- i))
(j (random (1+ i))(random (1+ i))))
((= i 1) data)
(swap (nth i data) (nth j data)))))
(defmacro swap (x y)
`(let ((temp ,x))
(setf ,x ,y)
(setf ,y temp)))
(defun rest ()
(let ((range (abs (- maxrest minrest))))
(s-rest (+ minrest (* range (rrandom))))))
(defun get-next-note (params)
(let ((note (tone (first params)))
(gain (second params)))
(seq (rest)
(cue (mult gain note)))))
(let ((data (shuffle (paramlist))))
(seqrep (i (length data))
(get-next-note (nth i data))))
Big, big thanks 
this code is working perfectly
Hi I have one issue to discuss. Is it possible to create a particular step in radomization of silence in this code ? If I generate the randomized silence from this code the duration of silence the most oftenly appears to be 2,2 s and more randomized silence is needed so the listener of this soundtrack could be able not to get used to duration of silence. Thanks for discussing the topic. And one another topic. If I want to have the information about all particulars levels of sounds, duration of silences between them and the frequency of the sounds in the sequence without following the whole track and doing it manually, I think it’s enough to use just a command print after all of these functions, am I right ?
Check your statistical analysis.
To print a list of the randomised spacing to the debug window, try something like this:
(defun rest ()
(let ((range (abs (- maxrest minrest)))
dur)
(print (setq dur (+ minrest (* range (rrandom)))))
(s-rest dur)))
Yeah, that was what my academic told me about the duration of silence. I checked the statistics and I have no idea what he was talking about, because it’s very random in my opinion. Could you give me some tips about another question ?
If I want to have the information about all particulars levels of sounds and the frequency of the sounds in the sequence without following the whole track and doing it manually, I think it’s enough to use just a command print after all of these functions, am I right >
> ?
Should I do that by an analogy to the example you posted ?
“PRINT” is a useful command for printing out a single value. If it is the final command in a script, then the printed text (a “string”) will be the return value from the code and will be displayed in a pop-up window. The PRINT command also prints to the debug window.
A more flexible way of printing is with the FORMAT command: XLISP format
When the “destination” is NIL, then it can be used to create a return value from the Nyquist script.
If the destination is “T”, then it prints to the debug window.
Example (run with the Debug button):
(setf a "Hello")
(setf b "World")
(format t "Output to debug: ~a ~a" a b)
(format nil "Return value ~a ~a" b a)
To be honest, I’ve been trying to get the information about all particulars levels of sounds and the frequency of the sounds in the sequence by printing it in debug window, but I have problems with realisation of that issue also
In this post:: https://forum.audacityteam.org/t/adding-randomized-silence-windows-10-audacity-2-1-3/46301/45
Look at the last few lines:
(let ((data (shuffle (paramlist))))
(seqrep (i (length data))
(get-next-note (nth i data))))
This creates a local variable called “data” which is set to the value of, the generated “paramlist” (list of parameters) after it has been shuffled.
We then create a sequence of sounds from that “data” list by sending each item from the list in turn to the function “get-next-note”.
If we print that data, we see that it is a list containing pairs of values. The first of that pair is the pitch (as a MIDI note number), and the second of each pair is the amplitude (linear amplitude on a scale of 0 to 1).
So the simplest way to get the data, is to just print that “data” variable:
(let ((data (shuffle (paramlist))))
(print data)
(seqrep (i (length data))
(get-next-note (nth i data))))
It’s probably not in a very convenient form, given that it is “MIDI Note number” and “linear amplitude”, but it is the data, and it will look something like this:
((83.2131 0.01) (107.213 0.562341) (83.2131 0.01) (107.213 0.0177828) (83.2131 0.316228) (107.213 0.00562341) (107.213 0.177828) (107.213 0.01) (83.2131 0.0177828) (107.213 1) (107.213 0.0562341) (107.213 0.0316228) (107.213 0.1) (83.2131 0.00562341) (83.2131 0.316228) (83.2131 0.01) (83.2131 0.01) (83.2131 0.562341) (107.213 0.01) (83.2131 0.0316228) (83.2131 0.316228) (83.2131 0.0177828) (83.2131 0.01) (107.213 0.01) (83.2131 0.0177828) (83.2131 0.0177828) (83.2131 0.0562341) (83.2131 0.0562341) (107.213 0.0562341) (83.2131 0.562341) (83.2131 1) (83.2131 0.562341) (107.213 0.00562341) (83.2131 0.316228) (83.2131 0.0177828) (83.2131 0.562341) (107.213 0.316228) (107.213 0.00562341) (83.2131 0.1) (107.213 0.316228) (83.2131 0.0177828) (83.2131 0.00562341) (83.2131 0.177828) (107.213 0.0316228) (83.2131 1) (107.213 0.316228) (83.2131 0.1) (107.213 0.0177828) (107.213 0.1) (83.2131 0.1) (83.2131 0.562341) (107.213 1) (107.213 0.1) (83.2131 0.316228) (83.2131 0.0562341) (83.2131 1) (83.2131 1) (83.2131 0.01) (83.2131 1) (83.2131 0.00562341) (107.213 0.177828) (107.213 0.01) (83.2131 1) (107.213 0.00562341) (107.213 0.562341) (83.2131 0.0177828) (107.213 1) (83.2131 0.0316228) (107.213 0.177828) (107.213 0.0562341) (107.213 0.316228) (83.2131 0.1) (107.213 0.562341) (107.213 0.1) (107.213 0.1) (107.213 1) (107.213 0.177828) (107.213 0.01) (107.213 0.0562341) (83.2131 0.01) (83.2131 0.1) (83.2131 0.00562341) (107.213 1) (83.2131 0.0562341) (107.213 0.562341) (83.2131 0.00562341) (83.2131 0.0562341) (107.213 1) (83.2131 0.316228) (83.2131 0.00562341) (107.213 0.0316228) (83.2131 0.01) (107.213 0.00562341) (107.213 0.0177828) (107.213 1) (83.2131 0.177828) (83.2131 0.562341) (107.213 0.01) (107.213 0.0316228) (107.213 0.1) (83.2131 0.0316228) (83.2131 0.562341) (83.2131 0.0562341) (107.213 0.562341) (83.2131 0.0177828) (83.2131 0.1) (83.2131 0.00562341) (83.2131 0.0562341) (83.2131 0.1) (107.213 0.562341) (83.2131 0.1) (83.2131 0.177828) (83.2131 0.177828) (107.213 0.0177828) (107.213 0.0562341) (83.2131 0.01) (83.2131 0.316228) (107.213 0.177828) (83.2131 0.0316228) (83.2131 0.0316228) (83.2131 0.0177828) (83.2131 0.0316228) (83.2131 0.0177828) (107.213 0.0562341) (83.2131 0.177828) (107.213 0.00562341) (83.2131 0.316228) (83.2131 0.177828) (83.2131 0.0562341) (107.213 0.177828) (107.213 0.0562341) (107.213 0.1) (107.213 0.0316228) (83.2131 0.0316228) (107.213 0.1) (83.2131 0.562341) (107.213 0.316228) (83.2131 1) (83.2131 0.1) (107.213 0.316228) (107.213 0.562341) (83.2131 0.562341) (107.213 0.0316228) (107.213 0.316228) (83.2131 0.0316228) (83.2131 0.0562341) (107.213 0.01) (107.213 0.01) (107.213 0.0562341) (107.213 0.0177828) (107.213 0.00562341) (107.213 0.177828) (107.213 0.0177828) (107.213 0.0316228) (107.213 1) (107.213 1) (83.2131 0.00562341) (83.2131 0.177828) (83.2131 0.177828) (107.213 0.177828) (107.213 0.0316228) (83.2131 0.562341) (107.213 0.01) (107.213 0.0177828) (107.213 0.1) (83.2131 0.316228) (83.2131 1) (83.2131 0.316228) (83.2131 0.1) (107.213 0.0177828) (107.213 0.562341) (107.213 0.0562341) (107.213 0.0177828) (107.213 1) (107.213 0.00562341) (83.2131 0.177828) (83.2131 0.0562341) (107.213 0.00562341) (83.2131 0.0316228) (107.213 0.1) (107.213 0.562341) (83.2131 0.00562341) (83.2131 0.177828) (107.213 0.0316228) (107.213 0.177828) (107.213 0.0562341) (107.213 0.0177828) (83.2131 0.0316228) (83.2131 1) (107.213 0.01) (83.2131 0.01) (107.213 0.177828) (83.2131 1) (107.213 0.00562341) (83.2131 0.00562341) (107.213 0.316228) (107.213 0.316228) (107.213 0.316228) (107.213 0.562341) (107.213 0.0316228))
If you know how to use Excel, then it should not be too difficult to convert that into a more convenient form, such as “Hz” and “dB”, or we could do that in Nyquist.
To do that in Nyquist, we would need a function like this:
(defun printdata (data)
(format t " Hz\t dB~%")
(do* ((id 0 (1+ id))
(param (first data)(nth id data)))
((= id (length data)))
(format t "~a\t ~a~%"
(round (step-to-hz (first param)))
(round (linear-to-db (second param))))))
and then call it from the sequence generator like this:
(let ((data (shuffle (paramlist))))
(printdata data)
(seqrep (i (length data))
(get-next-note (nth i data))))
The only thing that doesn’t give us is the length of the gaps. These are generated on the fly by the sequence generator, so the easiest way to capture those is to print them as they are generated - something like this:
(defun rest ()
(let ((range (abs (- maxrest minrest))))
(print (setf dur (+ minrest (* range (rrandom)))))
(s-rest dur)))
Another way would be to print all of the parameters as each note is created.
This would require modifying the REST function so that it returns both the required silence and the length of the silence (for example, as a list:
(defun rest ()
(let* ((range (abs (- maxrest minrest)))
(dur (+ minrest (* range (rrandom)))))
(list (s-rest dur) dur)))
and modifying GET-NEXT-NOTE so that it sends each of its parameters to a print function before returning the next note:
(defun get-next-note (params)
(let ((note (tone (first params)))
(gain (second params))
(rest-data (rest)))
(prettyprint (first params)
(second params)
(second rest-data))
(seq (first rest-data)
(cue (mult gain note)))))
and a print function:
(defun prettyprint (pitch gain time)
(format t "~a Hz \t ~a dB \t ~a s~%"
(round (step-to-hz pitch))
(round (linear-to-db gain))
time))
Optionally, you can set the print format for floating point numbers, for example, to print with 4 decimal places:
(setf *float-format* "%.4f") ; 4 decimal places when printing floats.
(let ((data (shuffle (paramlist))))
(seqrep (i (length data))
(get-next-note (nth i data))))
and the output looks something like this:
4000 Hz -40 dB 2.4588 s
4000 Hz -30 dB 2.1386 s
1000 Hz 0 dB 2.2297 s
1000 Hz -25 dB 2.0263 s
1000 Hz -5 dB 2.5403 s
4000 Hz -25 dB 2.7308 s
4000 Hz -30 dB 2.5617 s
4000 Hz 0 dB 2.4747 s
4000 Hz -35 dB 2.6911 s
1000 Hz -10 dB 2.4533 s
1000 Hz -35 dB 2.1131 s
1000 Hz -10 dB 2.3937 s
1000 Hz -35 dB 2.5357 s
4000 Hz -20 dB 1.9627 s
4000 Hz -40 dB 2.1491 s
4000 Hz -35 dB 2.0885 s
1000 Hz -5 dB 2.6064 s
4000 Hz -45 dB 1.8044 s
4000 Hz -20 dB 2.3961 s
4000 Hz -15 dB 2.4370 s
4000 Hz -45 dB 2.3061 s
1000 Hz -40 dB 2.0958 s
1000 Hz -25 dB 2.6446 s
1000 Hz -35 dB 1.8709 s
4000 Hz -5 dB 2.0352 s
4000 Hz -20 dB 1.8108 s
4000 Hz -45 dB 2.7969 s
4000 Hz -45 dB 2.4882 s
4000 Hz -30 dB 2.2427 s
4000 Hz -35 dB 2.1297 s
1000 Hz -30 dB 2.0012 s
4000 Hz -30 dB 2.2447 s
1000 Hz -40 dB 2.7369 s
4000 Hz 0 dB 1.8263 s
1000 Hz -30 dB 2.0860 s
1000 Hz -35 dB 2.2875 s
1000 Hz -15 dB 1.8968 s
1000 Hz -45 dB 2.1889 s
4000 Hz -45 dB 2.4929 s
1000 Hz 0 dB 2.1025 s
4000 Hz -30 dB 1.9990 s
1000 Hz 0 dB 2.1677 s
1000 Hz -15 dB 2.5698 s
4000 Hz -10 dB 2.6625 s
1000 Hz -20 dB 2.4326 s
1000 Hz -15 dB 1.8977 s
4000 Hz -40 dB 2.4434 s
1000 Hz 0 dB 1.8946 s
4000 Hz -35 dB 2.1316 s
4000 Hz -20 dB 2.5927 s
4000 Hz -25 dB 1.9224 s
4000 Hz -45 dB 1.9838 s
1000 Hz -10 dB 2.6107 s
4000 Hz -20 dB 1.8097 s
1000 Hz -40 dB 2.3934 s
4000 Hz -40 dB 2.2973 s
4000 Hz -25 dB 2.2261 s
1000 Hz -35 dB 2.6861 s
1000 Hz -30 dB 2.0632 s
1000 Hz -15 dB 1.9964 s
1000 Hz -25 dB 2.5373 s
4000 Hz -5 dB 2.1953 s
4000 Hz -25 dB 2.3071 s
4000 Hz -35 dB 2.2389 s
4000 Hz -25 dB 1.9397 s
4000 Hz -25 dB 2.3534 s
1000 Hz -40 dB 2.3165 s
1000 Hz -35 dB 2.4697 s
1000 Hz -30 dB 2.4111 s
4000 Hz -10 dB 2.3937 s
1000 Hz -5 dB 2.6889 s
1000 Hz -25 dB 2.5775 s
4000 Hz -15 dB 2.4995 s
1000 Hz -45 dB 2.5093 s
1000 Hz -45 dB 2.5452 s
4000 Hz -45 dB 2.0065 s
1000 Hz 0 dB 1.9714 s
1000 Hz -15 dB 2.6084 s
1000 Hz -45 dB 2.2346 s
4000 Hz -45 dB 1.8048 s
1000 Hz -45 dB 1.9718 s
1000 Hz -40 dB 2.2001 s
1000 Hz -5 dB 2.6376 s
1000 Hz -30 dB 2.6390 s
1000 Hz -35 dB 2.0564 s
4000 Hz -30 dB 2.1924 s
4000 Hz -35 dB 2.5729 s
1000 Hz -5 dB 1.8621 s
1000 Hz -45 dB 2.1840 s
1000 Hz -35 dB 2.5163 s
4000 Hz -35 dB 2.7778 s
4000 Hz 0 dB 2.4052 s
4000 Hz -20 dB 2.5553 s
4000 Hz -25 dB 2.1047 s
1000 Hz -15 dB 2.4536 s
4000 Hz 0 dB 1.8140 s
4000 Hz -15 dB 1.8062 s
4000 Hz -40 dB 2.0205 s
1000 Hz -40 dB 1.9775 s
1000 Hz -40 dB 2.1132 s
4000 Hz 0 dB 2.4121 s
1000 Hz -40 dB 2.5718 s
4000 Hz -5 dB 2.5839 s
1000 Hz -20 dB 1.9719 s
1000 Hz -25 dB 2.2629 s
4000 Hz -35 dB 1.8110 s
4000 Hz -15 dB 2.4885 s
4000 Hz -40 dB 2.2034 s
1000 Hz -15 dB 2.2614 s
4000 Hz -5 dB 2.2655 s
1000 Hz -30 dB 2.6454 s
4000 Hz -15 dB 2.7899 s
4000 Hz -40 dB 2.6232 s
4000 Hz -15 dB 1.8990 s
1000 Hz -25 dB 2.3785 s
1000 Hz -10 dB 2.3095 s
4000 Hz 0 dB 2.0321 s
1000 Hz -40 dB 2.3235 s
4000 Hz -10 dB 1.9906 s
4000 Hz -30 dB 2.5440 s
1000 Hz -20 dB 2.5293 s
4000 Hz -35 dB 2.4516 s
4000 Hz -45 dB 2.7012 s
1000 Hz -20 dB 1.8836 s
4000 Hz -15 dB 2.2026 s
1000 Hz -25 dB 2.5721 s
1000 Hz -30 dB 2.4842 s
1000 Hz -25 dB 2.0335 s
1000 Hz -45 dB 2.3675 s
1000 Hz -20 dB 1.8789 s
1000 Hz -30 dB 1.9670 s
4000 Hz -5 dB 2.5710 s
4000 Hz -20 dB 2.1718 s
1000 Hz -10 dB 2.6700 s
4000 Hz -10 dB 2.6813 s
1000 Hz -5 dB 2.0300 s
4000 Hz -10 dB 2.2048 s
1000 Hz 0 dB 2.3962 s
4000 Hz -25 dB 2.7034 s
1000 Hz -10 dB 1.9398 s
4000 Hz -40 dB 2.6610 s
1000 Hz -25 dB 2.0956 s
1000 Hz -5 dB 2.3903 s
1000 Hz -45 dB 2.0353 s
4000 Hz -10 dB 2.2915 s
1000 Hz -5 dB 2.7412 s
1000 Hz -40 dB 2.2037 s
1000 Hz -15 dB 2.5133 s
4000 Hz 0 dB 2.5192 s
4000 Hz -20 dB 2.7468 s
1000 Hz -15 dB 2.3003 s
4000 Hz -15 dB 1.8257 s
1000 Hz -5 dB 2.0713 s
1000 Hz -20 dB 2.7278 s
1000 Hz -15 dB 2.2284 s
4000 Hz 0 dB 2.2085 s
1000 Hz -35 dB 2.1097 s
1000 Hz -10 dB 1.9213 s
4000 Hz 0 dB 2.5146 s
4000 Hz -15 dB 2.7675 s
4000 Hz -10 dB 2.6634 s
1000 Hz 0 dB 1.9073 s
1000 Hz -30 dB 1.8693 s
1000 Hz 0 dB 2.2029 s
1000 Hz -20 dB 2.7268 s
1000 Hz -10 dB 2.4381 s
4000 Hz -30 dB 2.6680 s
1000 Hz -20 dB 2.0760 s
1000 Hz 0 dB 2.1711 s
1000 Hz -5 dB 2.3981 s
4000 Hz -30 dB 1.8903 s
1000 Hz -35 dB 2.2876 s
4000 Hz -10 dB 2.3906 s
4000 Hz -5 dB 2.3442 s
1000 Hz -10 dB 2.6619 s
1000 Hz -45 dB 2.2816 s
4000 Hz 0 dB 1.8032 s
1000 Hz -10 dB 2.6901 s
1000 Hz 0 dB 2.1745 s
4000 Hz -10 dB 1.8115 s
4000 Hz -40 dB 2.7969 s
4000 Hz -30 dB 1.8362 s
1000 Hz -45 dB 2.6603 s
4000 Hz -20 dB 2.7219 s
4000 Hz -5 dB 2.7296 s
4000 Hz -25 dB 2.1979 s
4000 Hz -45 dB 2.6564 s
4000 Hz -35 dB 2.1653 s
1000 Hz -20 dB 2.5244 s
4000 Hz -25 dB 2.5364 s
1000 Hz -25 dB 2.1057 s
4000 Hz -5 dB 2.1644 s
4000 Hz -20 dB 2.6338 s
4000 Hz -40 dB 2.6520 s
4000 Hz -5 dB 2.1876 s
1000 Hz -20 dB 2.1962 s
1000 Hz -30 dB 2.6692 s
4000 Hz -15 dB 2.1688 s
4000 Hz -5 dB 2.5593 s
4000 Hz -10 dB 2.4512 s
Thanks a lot It’s hard sometimes for me to understand a cause and effect relationship in the code while programming, cause I am a complete beginner.
The main thing to remember with Nyquist (and LISP), is that “functions” (code that does something) are always the first item inside the parentheses. A function may require additional “arguments”, which are supplied as a list after the name of the function:
(function-name arg1 arg2 arg3…)
Most functions return some kind of value, such as a number, a character, a string, an array, a list, a sound …
Example:
Name of function: SUM
Arguments: 1 and 2
Written as: (sum 1 2)
Return value: 3
To make a function do something, we must “call” the function. In the above example we “called” the function “SUM” and passed it two arguments, “1” and “2”.
Functions can call other functions. Often you will see this as “nested functions”.
Example:
(setf myanswer (sum (mult 2 3) (mult 4 5)))
Writing that with function names in upper case, and changing the layout, you can hopefully see how the nesting works:
(SETF myanswer
(SUM
(MULT 2 3)
(MULT 4 5)))
;sets the variable "myanswer" to 26 and returns 26
Hi After a huge break I have a question. Is it possible in Audacity to create stereophonic sound signals and is it possible to generate sound signal as a rectangular impulse which has a specified duration and amplitude ?
A note.
You can’t actually stop and start tones like turning on a switch.
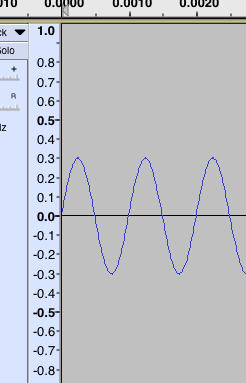
There is significant distortion at the stop and start points. It’s not pure tone. On pipe organs it’s call “chiff,” the difference between pressing the key and the time the note fully sounds. In electronics there are modulation effects that amount to the same thing.
Is this distortion going to affect the experiment?
Did I just uncover the reason you’re doing the experiment?
Koz
Yes, but you have to create a stereo track first.
Example:
- “Tracks menu > Add New > Stereo Track”
- Make an audio selection in the track
- “Effect menu > Nyquist Prompt” (Nyquist Prompt - Audacity Manual)
- Copy and paste this code into the Nyquist Prompt and click the OK button:
(abs-env
(vector (mult (pwlv 0 0.01 0.8 2 0)(noise 2))
(mult (pwlv 0 1.99 0.8 2 0)(noise 2))))
Yes.
Using the Nyquist Prompt again, say you want the pulse to be
- 0.01 seconds duration,
- amplitude 0.5,
- occurring after 1 second,
- with 2 seconds silence following the pulse:
(abs-env
(control-srate-abs *sound-srate*
(pwlv 0 1 0 1 0.5 1.01 0.5 1.01 0 3.01 0)))
The documentation:
http://www.cs.cmu.edu/~rbd/doc/nyquist/part8.html#index410
http://www.cs.cmu.edu/~rbd/doc/nyquist/part8.html#index582
http://www.cs.cmu.edu/~rbd/doc/nyquist/part8.html#index589
http://www.cs.cmu.edu/~rbd/doc/nyquist/part9.html#index867
Ok, I am gonna tell you about my experiment. It’s about examination of reaction times of people. Sounds appears on the base of a code in Nyquist language :
;version 4
;type generate
;; Global variables. These could be set by user controls.
(setf minrest 1.8)
(setf maxrest 2.8)
(setf lohz 1000)
(setf hihz 4000)
(defun tone (pitch)
(mult (osc pitch 0.25)
(pwlv 0 0.02 1 0.23 1 0.25 0)))
(defun paramlist (&aux params)
"Return a list of (pitch gain) pairs"
(dotimes (noteid 2 params)
(setf pitch (if (= noteid 0)
(hz-to-step lohz)
(hz-to-step hihz)))
(do ((gain 0 (- gain 5)))
((= gain -50))
(dotimes (i 10)
(push (list pitch (db-to-linear gain))
params)))))
(defun shuffle (data)
"Shuffle a list"
(let ((n (length data)))
(do* ((i (1- n) (1- i))
(j (random (1+ i))(random (1+ i))))
((= i 1) data)
(swap (nth i data) (nth j data)))))
(defmacro swap (x y)
`(let ((temp ,x))
(setf ,x ,y)
(setf ,y temp)))
(defun rest ()
(let* ((range (abs (- maxrest minrest)))
(dur (+ minrest (* range (rrandom)))))
(list (s-rest dur) dur)))
(defun get-next-note (params)
(let ((note (tone (first params)))
(gain (second params))
(rest-data (rest)))
(prettyprint (first params)
(second params)
(second rest-data))
(seq (first rest-data)
(cue (mult gain note)))))
(defun prettyprint (pitch gain time)
(format t "~a Hz \t ~a dB \t ~a s~%"
(round (step-to-hz pitch))
(round (linear-to-db gain))
time))
(setf *float-format* "%.4f")
(let ((data (shuffle (paramlist))))
(seqrep (i (length data))
(get-next-note (nth i data))))
This code was given here by steve. The experiment is about giving signals from this formula to first channel and on the second channel is supposed to be the rectangular signal to launch the clock of the reaction time measurement. I mean I’m thinking how to incorporate everything in code to couple appearing of the sound signal on the base of the formula with occuring this rectangular signal of duraton 10 ms and amplitude A (this amplitude is supposed to have a value to obtain a value of 4,5 - 5 V on the output of audiometer used to this experiment in the time before and after A=0). And this is how I think about launching the reaction time clock after sound signal appearing. Could anybody give me some help with this task ?