snd-xform BUG!!

Programming and Development Nyquist
1

I have been trying to write an effect that first cuts the input sound into ranges, then transforms certain of the pieces, then reassembles changed and unchanged pieces into a sequence.

I use snd-xform to select ranges of time and shift them to 0:

(defun extract-global (snd start end)
  (let* ((t0 (snd-t0 snd))
	 (result
	  (snd-xform snd (snd-srate snd) 0 (- start t0) (- end t0) 1.0)))
    result))

This should have the effect of making a little sound that “throws away” samples outside of the range.

Then I have a list of these little sounds, some of them further transformed and some not, and then I use shift-time (which is a thin function around snd-xform if you look at it with grindef) to put the pieces back in place and then I sum them.

It appears that some, but not all, of the un-transformed sounds improperly “remember” cycles that the first snd-xform should have cut off. And strangely, it looks like the end of the lengthened piece is not the original end of the selection, but what should be the end of some other one of the unchanged pieces. I suspect that when these twice snd-xform’d sounds evaluate, and they share the original sound in their data structures, there is some side effect on the original sound causing bad interactions.

I found that I can work around this by (1) returning

(prod -1.0 result)

instead from the function above and then (2) negating the final summation of pieces. I found that I do NOT get a successful workaround, if I just return

(prod 1.0 result)

or even if I try

(prod -1.0 (prod -1.0 result))

which makes me suspect that Nyquist is trying to do some “clever” simplifications of the sound objects before evaluating them, like detecting that multiplying by 1.0 is identity. But I suspect the cleverness goes wrong somewhere when sounds are supposed to be clipped by snd-xform, and I can foil this cleverness by negating the sound.

This explanation might not be clear, I haven’t found a simpler example that you can do in Nyquist prompt.

2

Here’s an easy Nyquist prompt experiment. It reveals that the bug depends not only on how my extracted sounds are defined and transformed, but also, THE SEQUENCE IN WHICH THEY ARE THEN PASSED TO sum.

First make a sine wave of 100 Hz, 1 second duration, 0.25 amplitude, and view it as Waveform. Select all and do this in Nyquist prompt.

    (defun extract-global (snd start end)
      (let* ((t0 (snd-t0 snd))
        (result
         (snd-xform snd (snd-srate snd) 0 (- start t0) (- end t0) 1.0)))
        result))

(let* (

(s1 (extract-global s 0.5 0.51))
(s2 (extract-global s 0.6 0.61))
(s3 (extract-global s 0.7 0.71))

(t1 s1)
(t2 s2)
(t3 s3)

(result (sum t1 t2 t3))

) (sum result (s-rest (get-duration 1))))

That picks out three cycles of the sound from various times, shifts all of them to time 0, and sums them with a silence that leaves the length of the selection unchanged. So, one cycle at 0 with amplitude 0.75 as expected.

Change three lines to this:

(t1 (shift-time s1 0))
(t2 (shift-time s2 0))
(t3 (shift-time s3 0))

And the effect is the same, as expected. Now try this:

(t1 (shift-time s1 0.5))
(t2 (shift-time s2 0.5))
(t3 (shift-time s3 0.5))

The lone tall cycle is at 0.5, as expected. But now try different shifts.

(t1 (shift-time s1 0.1))
(t2 (shift-time s2 0.2))
(t3 (shift-time s3 0.3))

Three separated cycles. Still unsurprising. But now make another change:

(result (sum t3 t2 t1))

There’s the bug! The sequence of evaluation of these sounds seems to matter. It looks like t1 is as it should be, but t2 ends where t3 should end, and t3 overlaps t2 for one cycle, and it ends… where the extract s2 began!

If the arguments to shift-time are all 0.5, then the result is correct with either sequence of arguments to sum. Or if you take the buggy version and change each of the t’s to (prod -1.0 (shift-time … ) ) then the behavior is as expected, no matter which sequence in sum.

3

[Update] This was written in response to the first post (you posted again while I was typing).

Normally you would use sound transformations rather than using snd-xform directly, so here’s a simple example of the same “bug” using the “at” and “extract” transformations.

(setf s1  (extract 0 0.5 s))
(setf s2  (extract 0 0.5 s))

(sim
  (at 0 (cue s1))
  (at 1 (cue s2)))

One would probably expect that the result should be the first half of “S”, followed by silence for half the duration of S, followed by the first half of S again, but that does not happen :astonished:

Although we appear to have created two new sound objects, S1 and S2, these are really just pointers to S.
Also. Nyquist uses lazy evaluation, so S1 and S2 are not evaluated until the end - we can prove this by modifying the code a little:

(setf s1  (extract 0 0.5 s))
(setf s2  (extract 0 0.5 s))

(sim
  (at 0 (cue s1))
  (at 1 (cue s2)))
(print "Hello World")

If we run this code with a very long selection, and watch the computer resources, we will notice that RAM and CPU usage are virtually nothing. S1 and S2 are not evaluated at all in this second example!

We know that “extract” returns the sound between “start” and “stop” relative to the current warp, but because, in our first example, it is not being evaluated until the end, “stop” is not known until after the expression has been evaluated.
There is a brief note in the manual regarding this:

Note: > Due to some internal confusion between the specified starting time and the actual starting time of a signal after clipping, stop is not fully implemented.

One way that we can work round the ambiguity of the stop time is to force S2 to be evaluated before evaluating the final expression, for example:

(setf s1  (extract 0 0.5 s))
(setf s2  (sum 0 (extract 0 0.5 s)))

(sim
  (at 0 (cue s1))
  (at 1 (cue s2)))

Another way is to explicitly define “stop” in the final expression, for example:

(setf s1  (extract 0 0.5 s))
(setf s2  (extract 0 0.5 s))

(extract 0 1.5
  (sim
    (at 0 (cue s1))
    (at 1 (cue s2))))
4

You are not trying to tell me this bug is not a bug?

I found an example where the sound returned by sum depends on the sequence of the summands. If I am encouraged to think about sound objects in mostly “functional programming” terms (so long as I don’t use snd-fetch, snd-fetch-array, or snd-fft), then this is certainly not expected behavior. Nor do I understand how the behavior with the summands scaled by -1.0, and without the scaling, can both be correct.

5

I tried transforming my t1, t2, t3, with (sum 0 …) and that does fix the “bug.” But (prod 1 …) does not fix the “bug.” Justify that behavior.

Can we drop the quotation marks from “bug” please?

6

I was quoting your use of the term, but I’m not convinced that it is a bug (and certainly not a capitalised BUG :wink:)

I totally agree that there is some very confusing behaviour when using snd-xform related functions, but the whole issue of warp, Environment, and Behaviours is rather confusing, and more so due to the way that Nyquist interacts with Audacity.

One example of a related behaviour that I think IS a bug can be demonstrated with the following code (applied to a stereo track):

(vector (aref s 0)(aref s 0))

but this is a bug in Audacity rather than in Nyquist.

By the way, regarding the issue that you raised about Audacity freezing when Nyquist returns an empty array; I submitted a patch that has now been committed so that returned arrays are validated. In the current SVN alpha version, returning an empty array will generate an error rather than freezing - this will be in the next release version of Audacity. I’ve not got a fix for the issue with negative sample rates, but I also raised that on the developers mailing list and Roger Dannenberg has said that he’ll take a look.

7

You have not persuaded me that there is a sensible user model justifying all of this observed behavior. Explain why wrapping terms in (sum 0 …) fixes the “bug” but (prod 1 … ) does not. I do not see a coherent user model here.

I find the global variables and environments and the local/global time distinctions more annoyance than help, so I am trying to go around them to the documented behavior of the snd- functions whenever I can to get done what I need done. And I tell you snd-xform is not behaving as documented if it has these problems with order of evaluation.

With the function grindef in the Nyquist prompt, you can see how extract and cue and cue-sound and shift-time are implemented in terms of snd-xform. There is nothing in extract that sets the global variable STOP. There is only a use of the parameter called STOP. You confuse these. Your last example, while hacking around the bug (bug, BUG!!! I say) in snd-xform, does not correctly explain WHY it works. I say it’s a mysterious accident that it works, just as it’s a mysterious accident that (sum 0 … ) works and (prod 1 … ) does not, none of it explicable by the manuals.

I thought the global variables and environments that I avoid using affect only the layer of stuff written in LISP that I can dump with grindef, and not the internals of the snd- functions.

8

I see that cue calls cue-sound which uses START and STOP which default to minus and plus 10^21.

Extract does not use them. shift-time uses different variables called MIN-START-TIME and MIN-STOP-TIME (no stars in names) as infinities to pass into snd-xform. They have the same default values as START and STOP.

None of these functions works by MODIFYING those globals.

Again this suggests that that these globals are used to give values to snd-xform, but are not supposed to influence what happens inside snd-xform or what happens at the later time of evaluation of the samples.

I understand snd-xform creates an object embodying a rule for lazy evaluation of samples. I understand that the rule is supposed to be completely well defined at the time snd-xform returns and is not supposed to change at the evaluation time. What I observe fails to conform to that. I don’t believe what I am observing is sensible intentioned behavior and not a bug.

9

OK, let’s take a different approach.

The source code says:

snd_xform – return a sound with transformations applied.

The “logical” sound starts at snd->time and runs until some
as yet unknown termination time. (There is also a possibly
as yet unknown logical stop time that is irrelevant here.)
The sound is clipped (zero) until snd->t0 and after snd->stop,
the latter being a sample count, not a time_type.
So, the “physical” sound starts at snd->t0 and runs for up to
snd->stop samples (or less if the sound terminates beforehand).

The snd_xform procedure operates at the “logical” level, shifting
the sound from its snd->time to time. The sound is stretched as
a result of setting the sample rate to sr. It is then (further)
clipped between start_time and stop_time. If initial samples
are clipped, the sound is shifted again so that it still starts
at time. The sound is then scaled by scale.

To support clipping of initial samples, the “physical” start time
t0 is set to when the first unclipped sample will be returned, but
the number of samples to clip is saved as a negative count. The
fetch routine SND_flush is installed to flush the clipped samples
at the time of the first fetch. SND_get_first is then installed
for future fetches.

An empty (zero) sound will be returned if all samples are clipped.

If I run the code (as a test example):

(let ((sound s)
      (sr *sound-srate*)
      (time 0)
      (start 1.25)
      (stop 3.5)
      (scale 1))
  (snd-xform sound sr time start stop scale))

then SND-XFORM behaves exactly as advertised. Do you agree?

Now what happens if we change “time”?
This gets a bit peculiar in Audacity because the start time for returned sounds is always zero. (Note that Nyquist was written as a standalone programming language that was shoehorned into Audacity to provide a simple but powerful tool for rapid development of experimental plug-ins).

(let ((sound s)
      (sr *sound-srate*)
      (time 2)
      (start 1.25)
      (stop 3.5)
      (scale 1))
  (snd-xform sound sr time start stop scale))

In this case, the start time is shifted by Nyquist to 2.0, but when the sound is returned to Audacity, the start time is zero. The act of returning the sound to Audacity has shifted the sound backward to zero.

We can counteract this shift by giving Audacity a “time = 0” reference:

(let ((sound s)
      (sr *sound-srate*)
      (time 2)
      (start 0)
      (stop 5)
      (scale 1))
  (sum (s-rest 1)
  (snd-xform sound sr time start stop scale)))

Now we get the expected behaviour.

As an example - generate a 10 second “Chirp” and apply the above code and the result is (as expected):
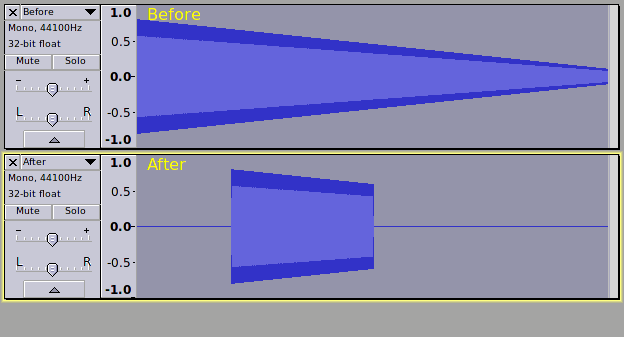
tracks001.png
Let’s modify the code a little:

(let ((sound s)
      (sr *sound-srate*)
      (time 2)
      (start 0)
      (stop 5)
      (scale 1))
  (sum (s-rest 0.5)
    (snd-xform sound sr time start stop scale)))

Again we get the expected result:
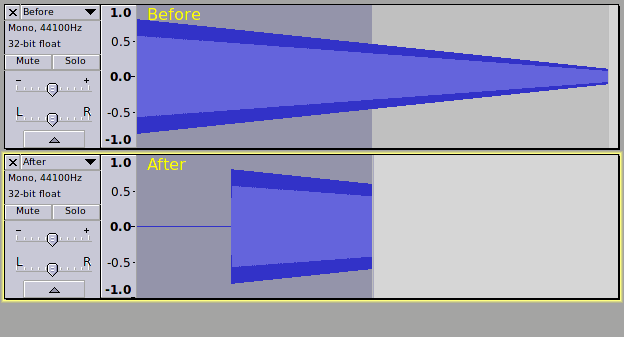
tracks002.png
Now let’s shorten the “s-rest” a little more:

(let ((sound s)
      (sr *sound-srate*)
      (time 2)
      (start 0)
      (stop 5)
      (scale 1))
  (sum (s-rest 0.4)
    (snd-xform sound sr time start stop scale)))

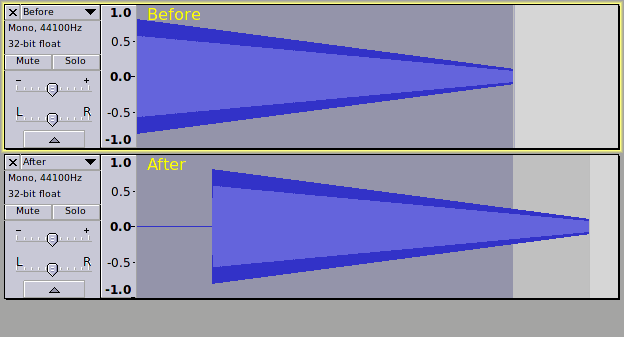
tracks003.png
We now have an appearance of “the bug”!
We expected that “sound” would stop at 5.0 seconds because we tried to clip it to 5.0 seconds. When we did this without SIM it worked fine, but for some reason SIM has messed it up! Why?

Simultaneous Behavior
http://www.cs.cmu.edu/~rbd/doc/nyquist/part4.html#27

Strictly speaking, this is wrong!
SIM returns a sound which is the sum of the given behaviours and as the manual stresses “sounds are not behaviors!”- usually we can get away with it, but not this time.

What happens if we (correctly) use CUE in the last example?

(let ((sound s)
      (sr *sound-srate*)
      (time 2)
      (start 0)
      (stop 5)
      (scale 1))
  (sum
    (cue (s-rest 0.4))
    (cue (snd-xform sound sr time start stop scale))))

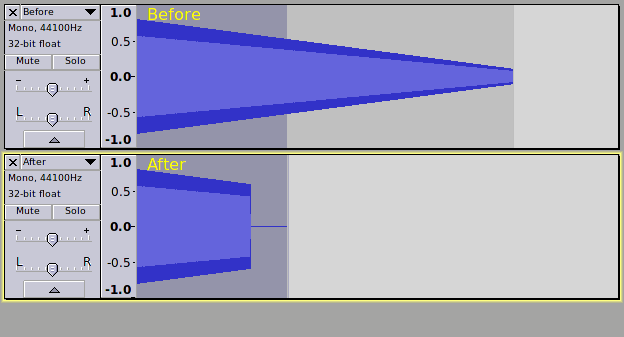
tracks005.png
It’s not what we wanted, but it has done the right thing. SIM (or SUM) plays both sounds starting at the same time.
What we actually wanted was to start “sound” at 2.0 seconds, so the “correct” code would be:

(let ((sound s)
      (sr *sound-srate*)
      (time 2)
      (start 0)
      (stop 5)
      (scale 1))
  (sum
    (cue (s-rest 0.4))
    (at-abs 2 
      (cue (snd-xform sound sr time start stop scale)))))

but this will not work!
We want snd-xform to set the start and stop time of “sound”, but we are overriding it with (SIM (AT-ABS (CUE … so snd-xform does not get evaluated.

To get this to work (and still be “correct”) we need to evaluate SND-XFORM using the start time and stop time of “sound”.
If we use SIM (or SUM) with a number and a sound, SND-OFFSET is used to perform the operation, and this will then evaluate our SND-XFORM function using the start time and stop time of “sound”.

(let ((sound s)
      (sr *sound-srate*)
      (time 2)
      (start 0)
      (stop 5)
      (scale 1))
  (sum
    (cue (s-rest 0.4))
    (at-abs 2 
      (cue (sum 0 (snd-xform sound sr time start stop scale))))))
10

I agree that sim is another name for sum.

I agree that your fifth example is the first one that surprises me.

I do not agree that what you then link to explains the behavior. In that example the “surprising” but explicable behavior involves seq, not sim. The “surprise” was that the actual start of one of the sounds is not delayed as expected. The surprise in our example is that the ending time of the extract is later than expected, not that the start time is earlier than expected.

I gave you an example in which the sequence of the arguments given to sum had an effect on the result. This is still not explained.

I gave an example in which the “bug” as I define it can be “fixed” by negating each summand with (prod -1.0 …) and then applying the same to the sum. No (sum 0 …) is used. I do not understand why this “works.”

11

I can get the entire definition of at-abs and cue in my Nyquist prompt. at-abs is only a Lisp macro that changes WARP while the second argument evaluates. That argument is a call to cue, which is a Lisp function that uses WARP to calculate the arguments to snd-xform.

In short the (at-abs (cue (snd-xform …))) expression is understandable as just a snd-xform of a snd-xform.

If anything explains the misbehavior (I am still leaving quotes off) of the ending time, it is the internals of sim, not anything in at-abs or cue.

12

If you wish to pursue this further I think that you will need to take it up with the developer (Roger B. Dannenberg, Carnegie Mellon University).

13

Yes.
http://www.cs.cmu.edu/~rbd/doc/nyquist/part8.html#index583
“(sim [beh1 beh2 …]) [LISP]”


http://www.cs.cmu.edu/~rbd/doc/nyquist/part4.html#index140
“sounds are not behaviors!”

14

If you will bear with one more example. Here is your fifth code example.

    (let ((sound s)
          (sr *sound-srate*)
          (time 2)
          (start 0)
          (stop 5)
          (scale 1))
      (sum (s-rest 0.4)
        (snd-xform sound sr time start stop scale)))

What I get is two seconds of silence and ten seconds of sound, but I think there should be only three seconds of sound. Now here is a modification.

    (let ((sound s)
          (multiplier -1.0) ; change
          (sr *sound-srate*)
          (time 2)
          (start 0)
          (stop 5)
          (scale 1))
      (sum (s-rest 0.4)
        (prod multiplier ; change
        (snd-xform sound sr time start stop scale))))

THIS does what I expect. Can you explain that?

Experiment with other values of the multiplier. They all seem to make a sound only 5 seconds long, except for a range of values near 1.0 but not all exactly 1.0. (0.9999999 “fixes” it but 0.99999999 does not.) Why does that make sense?

Multiplying a sound by 1 is an identity, and that would give the same effect as your fifth example. But 1 (and a small range near 1) seem to be treated as exceptional multipliers as regards the sound extent. And the adding of 0 with sum, a different thing that one also expects to be a mathematical identity, does NOT behave like mulitplying by 1, but DOES behave like multiplying by -1, or by 2, as regards the sound extent. This is all just weird and I don’t see the rationale. Unless there is no rationale and it’s a bug.


I do not believe the documentation you linked to provides a satisfactory explanation.

How can I communicate this to Roger? Or would you?

15

And by the way, Steve, thank you for bringing the other strange edge cases I found, of hangs or crashes in Audacity, to the developers’ attention. These reactions to stupid inputs I don’t mean to produce don’t affect me as much as this perplexity with snd-xform and sum, but it is good to know the program is a little more defensive against stupid inputs.

16

Well the code is still not “right” strictly speaking because it is treating sounds as behaviours, but it looks to me like it works because it is making Nyquist evaluate snd-xform before evaluating sim. Although it works in this case I expect that experts would cringe at relying on the order of execution within a lazy evaluation scheme.

In 32 bit float format 0.99999999 is exactly 1 (0x3f800000)

17

Very interesting. I tried the first example [with (result (sum t3 t2 t1))] in Nyquist, and I get the same results whether I sum t1 t2 t3 or t3 t2 t1. I’d be curious if you find the same thing, or I just did something wrong. I used (setf s (scale 0.25 (hzosc 100))) before the code to set s and I used (s-plot (test) 0.4) after the code to see the result.

If Nyquist and Audacity give different results, I would guess there’s something strange going on in the Audacity/Nyquist interface. There are in fact some tricky differences, especially that Audacity translates everything from the selection time to time=0, runs Nyquist, and translates back. This example is now on my list of things to look at, and I’ll let you know what I find.

The observations about multiplying by 1 are not surprising. Nyquist “knows” that multiplication by 1 is the identity, multiplication by 0 yields 0, and addition by 0 is a noop. It also knows some functions are linear, e.g. if you multiply (mult (scale 3 s1) (scale 4 s2)) the result is equivalent to (scale 12 (mult s1 s2)). The actual DSP code that runs is selected according to whether scaling is necessary, resampling is necessary, and which parameters are scalar and which are signals, so there’s a lot of dynamic optimization going on. When scale factors hit SUM, there’s not much Nyquist can do, so it generates a SND-SCALE unit generator to actually scale samples. At that point, you get a new sound and stop any potential sharing of samples.

I have no idea why multiplication has an effect, and that does seem wrong. There are some invalid programs in Nyquist, e.g. (seq (osc c4) (at-abs 0 (osc d4))) is invalid because by the time SEQ instantiates the second sound which starts at time 0, SEQ has already delivered 1 s of the first sound – it can’t go back in time and fix the samples. Since you are shifting sounds around in time with xform, it seems possible you’ve just written an invalid program, but since it looks OK and runs in Nyquist, we should look into it.

18

To be clear, my example doesn’t actually contain the misbehaving code all in one piece. For me the necessary conditions include (sum t3 t2 t1) and also

    (t1 (shift-time s1 0.1))
    (t2 (shift-time s2 0.2))
    (t3 (shift-time s3 0.3))

or other, differing shifts for the three sounds. I do not see the problem when the sounds are shifted by the same amount.

If Nyquist and Audacity give different results, I would guess there’s something strange going on in the Audacity/Nyquist interface. There are in fact some tricky differences, especially that Audacity translates everything from the selection time to time=0, runs Nyquist, and translates back.

I think the correct statement is: not time 0, but rather, whatever (snd-t0) of the returned sound is, is mapped back by Audacity to the time of the beginning of the selection.

Thus if I want to (1) extract one piece of a sound, which is shifted to 0, (2) shift it again to another time, then (3) return a sound that shows the effect of 2 – then I must add that sound to a silent sound that starts at 0. Otherwise the effect of (2) is lost. So further questions might be: is the problem already inherent after (2), where the result of snd-xform is sent again to snd-xform (as called by shift-time)? Or does the problem never occur with just one extracted sound no matter how many transformations, but only when two or more sounds are extracted from the shared input sound? If so, two extracts must be combined some way, as with sum. Is the misbehavior part of the implementation of sum, or the implementation of the sharing?

19

To be very explicit, here is a complete example of "misbehavior"for me. It assumes s is bound to some sound, it need not be a 100 Hz wave, the chirp that Steve used will do. (Incidentally I changed (s-rest (get-duration 1)) to (s-rest 1) which is more correct to leave the length of selection unchanged.) And again, reverse the sequence of the three summands and the result is more as expected.

        (defun extract-global (snd start end)
          (let* ((t0 (snd-t0 snd))
            (result
             (snd-xform snd (snd-srate snd) 0 (- start t0) (- end t0) 1.0)))
            result))

    (let* (

    (s1 (extract-global s 0.5 0.51))
    (s2 (extract-global s 0.6 0.61))
    (s3 (extract-global s 0.7 0.71))

    (t1 (shift-time s1 0.1))
    (t2 (shift-time s2 0.2))
    (t3 (shift-time s3 0.3))

    (result (sum t3 t2 t1))


    ) (sum result (s-rest 1)))
20

Thanks for the clarifications – in fact, I did shift s1, s2, and s3 by different time amounts and summed t1 t2 t3 in different orders; in fact, just for the record, here’s the code I ran in the NyquistIDE:

(setf s (scale 0.25 (hzosc 100)))

(defun extract-global (snd start end)
  (let* ((t0 (snd-t0 snd))
         (result
          (snd-xform snd (snd-srate snd) 0 
                     (- start t0) (- end t0) 1.0)))
    result))


(defun test ()
  (let* ((s1 (extract-global s 0.5 0.51))
         (s2 (extract-global s 0.6 0.61))
         (s3 (extract-global s 0.7 0.71))
         (t1 (shift-time s1 0.1))
         (t2 (shift-time s2 0.2))
         (t3 (shift-time s3 0.3))
         (result (sum t3 t2 t1)))
     (sum result (s-rest (get-duration 1)))))

(s-plot (test) 0.4)

I was about to speculate on what’s happening, but I think the right thing is to really figure it out and either fix the implementation or the documentation (or discover something we’ve overlooked and that Nyquist and Audacity are doing the right thing).