Hello,
I see that there are no decimal places for the frequencies and this seems like quite a limitation.
Do you mean in “Plot Spectrum”? http://manual.audacityteam.org/man/plot_spectrum.html
If so, the frequency analysis measures how much audio there is in a sequence of “frequency bands”. For example, with default settings, the frequency bands are:
0.000000 to 86.132812
86.132812 to 172.265625
172.265625 to 258.398438
258.398438 to 344.531250
...
...
21791.601562 to 21877.734375
21877.734375 to 21963.867188
21963.867188 to 22050.000000
The frequency values shown in the interface are then estimated by interpolation from the surrounding data values.
The estimated values are usually within about +/- 1 Hz, depending on the selected options. Higher “Size” settings give better frequency accuracy by collecting the “frequency bins” over longer periods of time.
Thanks, yes I do mean “plot spectrum”.
What you’ve told me is hard for me to understand. I really just want “cursor” and “peak” to at least one or two decimal places. It might be good also to be able to zoom in on the frequency axis like we can in the amplitude axis.
The approximation is not that accurate. It would be like if I asked you to measure with a ruler the length of a piece of string to thousandths of a mm, when in fact you could not actually measure more precisely than to about +/- half a mm.
I see. It should be possible to improve this in some cases though, and limiting the frequency precision the nearest hz is probably too blunt. I didn’t understand much of what you said earlier but I think that the frequency resolution for DFT will be basically proportional to the amount of data. I don’t know a formula for the error in the frequency though. I’d like to look into this later.
OK last post by me on this; I’ve managed to get two decimal points for frequency, I just had to select more data. The size is now 65,536, taken from from a 44.1khz wav file.
I did some reading and I think the frequency precision might be given by the following formula:
(input frequency) / N
Where N is the “size”. This seems to fit what I am seeing.
Yes, the bigger the “Size” setting in Plot Spectrum, the smaller the “frequency bins” (narrower frequency bands), so the more precise the Hz measurements.
At maximum “Size” (65536), the frequency bins are about 0.7 Hz wide, so in this case the approximation could be a little better than +/- 1 Hz, but why would you need that?
Hi sorry, ignore my last post. I looked at the scale and it had decimal points, but not the readings. I want the greater accuracy for checking musical notes. I think one or two hz can be quite significant. So it looks like I would like there to be a larger “size” setting.
Not if you only need to know what the note is. For example, with standard A440 tuning, an “A4” is nominally 440 Hz and an A#4 is about 466 Hz. If any real acoustic instrument plays an “A”, it will never be exactly 440 Hz. Unless you have exceptionally fine sense of pitch, any frequency around 440 Hz +/- a couple of Hz will sound like a correctly in-tune “A”.
Listen to this sequence of 8 notes (A, C#, A, G, C#, A, A, C#)
Which of the “A” notes sound in tune, which are a bit sharp, and which are a bit flat? Listen to it a few times and write down your answer before analyzing it.
I think one or two hz can be quite significant.
Why do you think that?
What instruments do you play? My joke is that I don’t play the piano, I play at the piano. Big difference.
Koz
My guess was that the second A was flat. I think the analyzer showed this, but as we were saying it’s probably just error and they are all the same. The analysis also had the last A being sharp, but the same applies.
For another example the difference between an E2 and an F2 is less than 5hz, so I would have thought that one or two hz would matter here. But my real application is to see if a backing track is slightly sharp/flat . If my guitar were also off in the other direction then I wonder if the effect would be quite significant.
Have you tried the “Pitch Detect” plug-in?
http://wiki.audacityteam.org/wiki/Nyquist_Analyze_Plug-ins#Pitch_Detect
(Download / install instructions: http://wiki.audacityteam.org/wiki/Download_Nyquist_Plug-ins#download)
Yes, but the “Size” for FFT refers to the size of the analysis window in samples. At 44100 Hz sample rate, the maximum Size of 65536 samples is nearly 1 ½ seconds, so unless the musical tempo is very slow, the spectrum will be that of several notes. Yes you could increase the sample rate, but that increases the range of the spectrum, which makes the ranges of the “bins” wider (the number of bins is half the “Size”, and the bins collectively cover the range from 0 Hz (DC offset) to half the sample rate (the “Nyquist” frequency).
Also, even down to C0, if you get a result that is correct to the nearest 1 Hz, you will get the right note.
(The lowest note of a double bass is usually E1, and most of the sound that you hear is higher harmonics of that).
That’s a good point about the note having to be long enough to analyze accurately.
When you say “to the nearest hz” though…hmmm, I would have thought the accuracy is +/-0.5 hz then. And the difference between C0 and c#0 is only 1.0 hz.
In any case, thanks for the discussion. I’m interested in trying to write my own plugin later on.
Guitar. For the low E, bending the note by a couple of hz is easy to hear.
And the errors could add up. An interval can of course be off by up to twice the error. This adds to any other errors, for example because we a using equal temperament.
Worth noting that with real-world sounds, there are always harmonics present. Although the frequency resolution of FFT gets progressively worse at lower frequencies, for many sounds it can be expected that the first harmonic will be exactly double the frequency of the fundamental. In terms of “pitch”, a more accurate estimate may be made by looking at the harmonics.
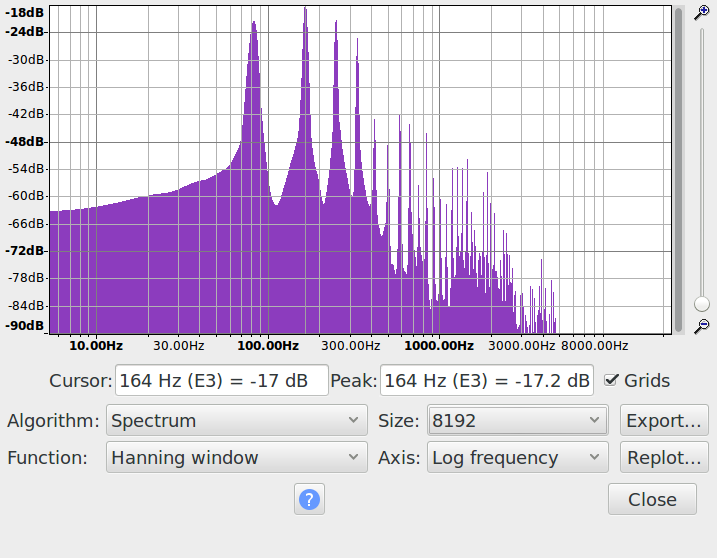
Example, in this spectrum the fundamental shows 83 Hz. Given the “Size” of 8192 samples and a sample rate of 44100 Hz, that figure lies between 80.749512 Hz and 86.132812 Hz, and the interpolated estimate is 83 Hz Here is the relevant part of the data (exported from Plot Spectrum):
64.599609 -50.531769
69.982910 -46.574673
75.366211 -32.057095
80.749512 -22.215677
86.132812 -24.367990
91.516113 -40.745335
96.899414 -50.853859
Looking at the first harmonic, the interpolated estimate is 164 Hz. Here is the data:
139.965820 -50.730862
145.349121 -48.354359
150.732422 -44.920811
156.115723 -34.589748
161.499023 -19.850306
166.882324 -18.712814
172.265625 -29.874290
177.648926 -45.561481
183.032227 -50.346607
Taking a naive approximation that the true value is somewhere between the mid-points of the adjacent bins, at 83 Hz, a range of +/- 2.6 Hz represents +/- 39.6 cents, but for the first harmonic, the accuracy improves to +/- 27.9 cents. If I recall correctly, Plot Spectrum uses cubic interpolation, so the approximation will actually be much better than this, but the same principle applies, that the first harmonic value is likely to be a better approximation than the fundamental.